Departments of Computer Science and Mathematics
Purdue University
The Cunningham Project:
Wagstaff is the leader of the Cunningham Project, whose goal is to factor numbers of the form bn±1. Wagstaff and hundreds of others around the world try to factor these special numbers. From time to time the latest factors are published in a book. The most recent such book appeared in 2002 and may be found at http://www.ams.org/online_books/conm22
See the official web site for the Cunningham Project at
http://homes.cerias.purdue.edu/~ssw/cun/index.html
for even more recent results.
The explicit factors of these numbers have many uses, including determining the length of the period of a decimal fraction, finding new perfect numbers, testing new integer factoring algorithms, discovering new algebraic identities like
2 (4k+2) + 1 = (2 (2k+1) - 2 k+1 + 1) (2 (2k+1) + 2 k+1 + 1),
and proving that large prime numbers really are prime. They also have many uses in cryptography from supplying large prime numbers to the efficient construction of enciphering devices such as linear feedback shift registers.
The Purdue IBM SP and Purdue and Notre Dame Intel clusters via Condor were used to factor numbers by the elliptic curve method, the quadratic sieve and the number field sieve.
An earlier computing project is shown below because of its still interesting graph .
Fractional Parts of the Bernoulli Numbers
The Bernoulli numbers are an infinite sequence of fractions. They alternate in sign. After a slow start, the absolute values of these numbers grow rapidly. The first few nonzero Bernoulli numbers are
1, -1/2, 1/6, -1/30, 1/42, -1/30, 5/66, -691/2370, 7/6, -3617/510, 43867/798, -174611/330.
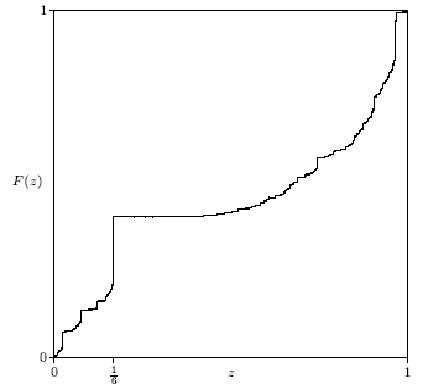
The fractional part of a real number is its excess above the next smaller whole number. For example, the factional parts of 286.23, - 1.1 and 3.1415926 are 0.23, 0.9 and 0.1415926. The graph shows the distribution function F(z) of the fractional parts of the Bernoulli numbers. That is, F(z) is the fraction of Bernoulli numbers with fractional part < z. One might expect the fractional parts of the Bernoulli numbers to be more or less random numbers between 0 and 1. If that were true, then the graph of F(z) would be a straight line from (0,0) to (1,1). As you can see from the graph, this is far from true.

Paul Erdös and Samuel S Wagstaff Jr, "The fractional parts of the Bernoulli numbers," Illinois J. Math. 24 (1980) 104-112, proved that the function F(z) is well defined and increases only by jumps. The jumps are dense in the unit interval (0,1). The largest jump is at z = 1/6. The second largest jump is at z = 29/30. The graph looks horizontal from z = 1/6 to about z = 0.3, but in fact it has tiny jumps everywhere between 0 and 1. Erdös and Wagstaff proved that if z is the fractional part of some Bernoulli number (other than z = 0 or z = 1/2), then infinitely many Bernoulli numbers (in fact, a positive fraction of them) have fractional part z. The graph indicates that about 15% of all Bernoulli numbers have fractional part 1/6.
Last updated 12/18/07